给定一张n个点m条边的无向图,每个点有权值$a_i$,现在可以任意加边,要求最小化$\sum_{i=1}^n(a_i-dist_i)^2$,其中$dist_i$表示1到i点的最短路$n \leq 40,m \leq 1600$
任意加边并不代表每个点的的$dist_i$都可以任意,仍然要满足一下条件$dist_1 = 0$$dist_i \not = 0, i \not= 1$$|dist_i-dist_j| \leq 1,(i,j) \in E$
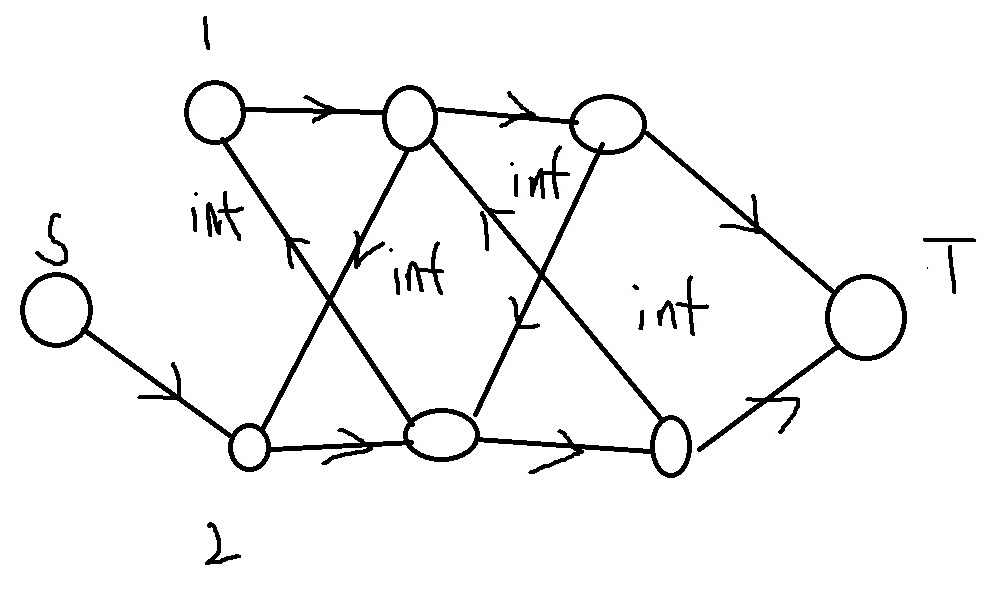
考虑对每个点拆成n-1个点,S和第一个点相连,第i个点和第i+1个点相连,第n-1个点和T相连,边权即为$(a_i-j)^2$,由于$dist_1=0$,所以直接让1拆出的第一个点和S不连边,最后再加上$a_i^2$的贡献。再考虑第三个限制,如果i和j有边,就让i拆出的第x个点向j拆出的第x-1个点连边,j同理。这样如果割掉i点拆出的x和x+1之间的边,就表示$dist_i=x$,并且此时对于和i有边的j,必须割掉x-1和x或者x和x+1或者x+1和x+2这三条边之一。所以这样建图再跑最小割即可。